1.Rational Numbers
Rational Numbers
A number is called Rational if it can be expressed in the form p/q where p and q are integers (q > 0). It includes all natural, whole number and integers.
Example: 1/2, 4/3, 5/7,1 etc. 
Natural Numbers
All the positive integers from 1, 2, 3,……, ∞.
Whole Numbers
All the natural numbers including zero are called Whole Numbers.
Integers
All negative and positive numbers including zero are called Integers.
Properties of Rational Numbers
1. Closure Property
This shows that the operation of any two same types of numbers is also the same type or not.
a. Whole Numbers
If p and q are two whole numbers then
Operation | Addition | Subtraction | Multiplication | Division |
Whole number | p + q will also be the whole number. | p – q will not always be a whole number. | pq will also be the whole number. | p ÷ q will not always be a whole number. |
Example | 6 + 0 = 6 | 8 – 10 = – 2 | 3 × 5 = 15 | 3 ÷ 5 = 3/5 |
Closed or Not | Closed | Not closed | Closed | Not closed |
b. Integers If p and q are two integers then
Operation | Addition | Subtraction | Multiplication | Division |
Integers | p+q will also be an integer. | p-q will also be an integer. | pq will also be an integer. | p ÷ q will not always be an integer. |
Example | - 3 + 2 = – 1 | 5 – 7 = – 2 | - 5 × 8 = – 40 | - 5 ÷ 7 = – 5/7 |
Closed or not | Closed | Closed | Closed | Not closed |
c. Rational Numbers
If p and q are two rational numbers then
Operation | Addition | Subtraction | Multiplication | Division |
Rational Numbers | p + q will also be a rational number. | p – q will also be a rational number. | pq will also be a rational number. | p ÷ q will not always be a rational number |
Example | 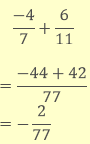
| 
| 
| p ÷ 0 = not defined |
Closed or Not | Closed | Closed | Closed | Not closed |
2. Commutative Property
This shows that the position of numbers does not matter i.e. if you swap the positions of the numbers then also the result will be the same.
a. Whole Numbers
If p and q are two whole numbers then
Operation | Addition | Subtraction | Multiplication | Division |
Whole number | p + q = q + p | p – q ≠ q – p | p × q = q × p | p ÷ q ≠ q ÷ p |
Example | 3 + 2 = 2 + 3 | 8 –10 ≠ 10 – 8 – 2 ≠ 2 | 3 × 5 = 5 × 3 | 3 ÷ 5 ≠ 5 ÷ 3 |
Commutative | yes | No | yes | No |
3. Associative Property
This shows that the grouping of numbers does not matter i.e. we can use operations on any two numbers first and the result will be the same.
a. Whole Numbers
If p, q and r are three whole numbers then
Operation | Addition | Subtraction | Multiplication | Division |
Whole number | p + (q + r) = (p + q) + r | p – (q – r) = (p – q) – r | p × (q × r) = (p × q) × r | p ÷ (q ÷ r) ≠ (p ÷ q) ÷ r |
Example | 3 + (2 + 5) = (3 + 2) + 5 | 8 – (10 – 2) ≠ (8 -10) – 2 | 3 × (5 × 2) = (3 × 5) × 2 | 10 ÷ (5 ÷ 1) ≠ (10 ÷ 5) ÷ 1 |
Associative | yes | No | yes | No |
b. Integers
If p, q and r are three integers then
Operation | Integers | Example | Associative |
Addition | p + (q + r) = (p + q) + r | (– 6) + [(– 4)+(–5)] = [(– 6) +(– 4)] + (–5) | Yes |
Subtraction | p – (q – r) = (p – q) – r | 5 – (7 – 3) ≠ (5 – 7) – 3 | No |
Multiplication | p × (q × r) = (p × q) × r | (– 4) × [(– 8) ×(–5)] = [(– 4) × (– 8)] × (–5) | Yes |
Division | p ÷ (q ÷ r) ≠ (p ÷ q) ÷ r | [(–10) ÷ 2] ÷ (–5) ≠ (–10) ÷ [2 ÷ (– 5)] | No |
c. Rational Numbers
If p, q and r are three rational numbers then
Operation | Integers | Example | Associative |
Addition | p + (q + r) = (p + q) + r | 
| yes |
Subtraction | p – (q – r) = (p – q) – r | 
| No |
Multiplication | p × (q × r) = (p × q) × r | 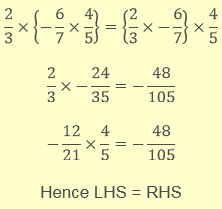
| yes |
Division | p ÷ (q ÷ r) ≠ (p ÷ q) ÷ r | 
| No |
The Role of Zero in Numbers (Additive Identity)
Zero is the additive identity for whole numbers, integers and rational numbers.
| Identity | | Example |
Whole number | a + 0 = 0 + a = a | Addition of zero to whole number | 2 + 0 = 0 + 2 = 2 |
Integer | b + 0 = 0 + b = b | Addition of zero to an integer | False |
Rational number | c + 0 = 0 + c = c | Addition of zero to a rational number | 2/5 + 0 = 0 + 2/5 = 2/5 |
Rational Numbers between Two Rational Numbers
Method 1
Example
Find the rational number between 1/10 and 2/10.
Solution
As we can see that there are no visible rational numbers between these two numbers. So we need to write the equivalent fraction.
2/10 = 20/100((multiply the numerator and denominator by 10)
Hence, 2/100, 3/100, 4/100……19/100 are all the rational numbers between 1/10 and 2/10.
Method 2
Find the rational number between 1/10 and 2/10.
Solution
To find mean we have to divide the sum of two rational numbers by 2.
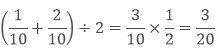
3/20 is the required rational numbers and we can find more by continuing the same process with the old and the new rational number.
Complete Chapter Notes And (Live) Classes Click below


